School of Computer Sciences
National Institute of Science Education and Research
Bhubaneswar

AutoBIM

Annada Prasad Behera | Subhankar Mishra's Lab

The AutoBIM project aims to integrate GIS information to existing BIM for populating BIM of a city with both geographic and geometric information. To that extent, the two goals of the project are (a) reconstruction of solid geometry from unstructured photographs; and (b) using mapping services to add location information.

The project member worked on reconstruction for the year 2020-2021 with data collected inside NISER, Bhubaneswar campus only (due to COVID-19 restrictions). One of the goals of reconstruction of models is novel views of a scene from a set of RGB images. The project memebr has tried the following,

• Single image reconstruction using differentiable renderers.
• Multiple image reconstruction mostly using COLMAP.
• Novel view synthesis using radiance fields.

The experimental results are given below, followed by the math behind the reconstruction.

• Annada Prasad Behera
• Subhankar Mishra (PI)

The video of the novel views is made from a subset of images given below. This is a very simple setup for a box on floor. A setup like this help extending the principles to more complex geometries. Note: The far-top part of the box is always missing for each novel view synthesized, even though they are present in every input image.

The animal house at NISER is a building hosted by the School of Biological Sciences. We tried to build novel views of the building using photographs from one side, to reduce complexity. The radiance field view synthesis is given above along with a subset the input images shown below.

The same animal house mesh is reconstructed as above, from photographs from all sides. This is a mesh reconstruction, rather than a radiance field reconstruction. The images below the video are (a) mesh with vertices and edges, (b) faces and; (c) textures. The video was created with Blender. Note: The back of the animal house is missing, not due to limitation of the algorithm but because of lack of photograph. We couldn't take pictures of the back because NISER's boundary was in the way.

Summary of the setup of how the above results were obtained.

	Box	Animal House
No. of images.	20	12
Machine	Lingaraj	Annapurna
Implementation	PyTorch CUDA 11.1	PyTorch CUDA 11.1
Training time	36 hours	20 hours
Iterations	500,000	25,000

	Lingaraj	Annapurna
CPU	Intel(R) Xeon(R) Gold 6138	AMD Ryzen Threadripper 3970X
GPU	4×NVIDIA GeForce RTX 2080 Ti	NVIDIA GeForce RTX 3090
Memory	512 GiB and 4×11 GiB (GPU)	60 GiB and 24 GiB (GPU)

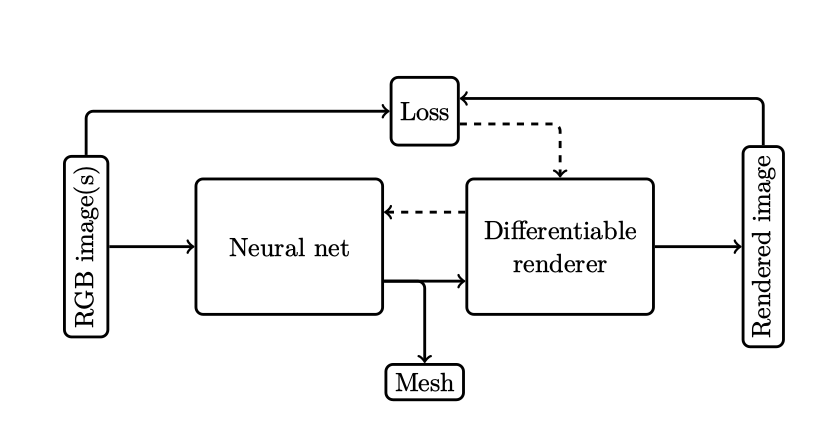
Each part of the above network is explained in the following sections.

• Encoder-decoder network.
• Input is 4 channel RGBA. Alpha for masking.
• Each linear and convolutional block output goes through a batch normalization and ReLU.

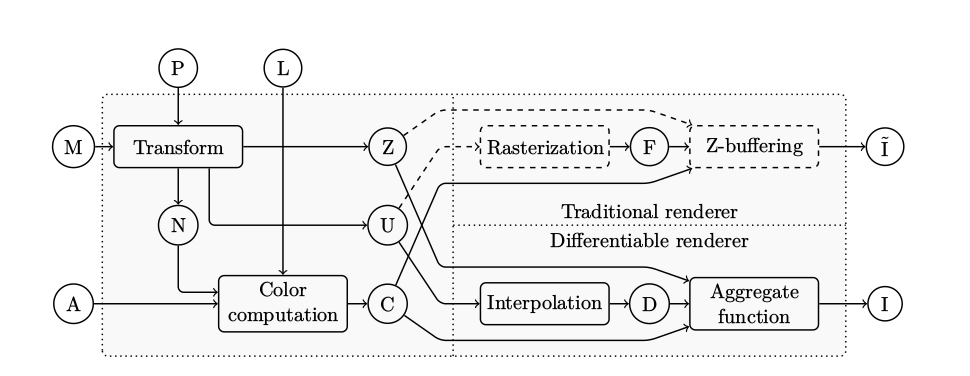
• Solid lines represent differentiable operation. Dashed lines not.
• \(P\) is camera, \(L\) is lights, \(M\) is the mesh, \(A\) is the mesh attribute, \(N\) is the normals, \(Z\) is the z-buffer, \(U\) is camera space co-ordinates, \(C\) is color, \(F\) is rasterized faces, \(D\) is the computation map, \(I\) and \(\tilde I\) are image output.
• Silhouette rasterization for background pixels and aggregate function. $$ A^j_i = \exp\bigg(-\frac{\text d(p_i, f_j)}{\delta}\bigg),\qquad A_i = 1-\prod_{n}^{j=1} (1-A^j_i) $$
• Barycentric interpolation, \(\Omega\) for the foreground pixel.
• Lights is done with the Phong lighting mode $$ I = I_c k_d(L\cdot N)+k_s(R\cdot V)^\alpha $$

Backpropagating the loss, $$ \frac{\partial I_i}{\partial u_k} = w_k,\qquad \frac{\partial I_i}{\partial u_k} = \sum_{m=0}^2 \frac{\partial I_i}{\partial w_m}\frac{\partial \Omega_m}{\partial v_k} $$ $$ \frac{\partial L}{\partial u_k} = \sum_{i=1}^N \frac{\partial L}{\partial I_i}\frac{\partial I_i}{\partial u_k},\qquad \frac{\partial L}{\partial v_k} = \sum_{i=1}^N \frac{\partial L}{\partial I_i}\frac{\partial I_i}{\partial v_k} $$

• $$L_\text{iou} = \mathbb E\bigg[ 1-\frac{||S\odot\tilde S||_1}{||S+\tilde S - S\odot \tilde S||_1} \bigg]$$
• $$ L_\text{color}=\mathbb E[||I-\tilde I||_1 ]$$
• $$L_\text{norm}= \sum_{e_i\in E} (\cos(\theta_i)+1)^2$$
• $$ L_\text{lap} = \bigg(\delta_v-\frac1{||N(v)||}\sum_{v'\in N(v)}\delta_{v'}\bigg)^2$$
The final loss is the weighted sum of the above losses.

Radiance field , \(F\) is a continuous 5D vector-valued function whose input is a 3D location \(r=(x, y, z)\) and a 2D viewing direction \((\theta, \varphi)\) and the output is an emitted color \(c=(r, g, b)\) and the volume density \(\rho\), $$ F_\Theta:(r,d)\to (c,\rho) $$

The color of any ray passing through the radiance field can be calculated using the classical volumetric rendering. The expected color \(C(r)\) of a camera ray \(r(t)=o+td\), starting at \(o\) and moving in the direction \(d\), from near bound \(t_n\) to the far bound \(t_f\) is, $$ C(r) = \int_{t_n}^{t_f} T(t)\rho(r(t))c(r(t), d)\ \text dt\\ $$ and $$ T(t) = \exp\bigg(-\int_{t_n}^{t_f}\rho(r(s))\ \text ds\bigg) $$

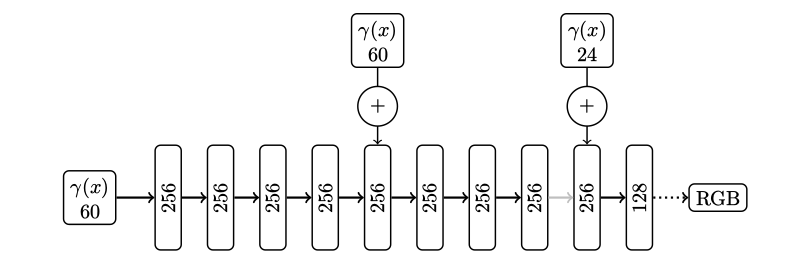
• Sampling $$ t_i \sim \mathcal U\bigg[ t_n+\frac{i-1}{N}(t_f-t_n),\ t_n+\frac{i}{N}(t_f-t_n)\bigg] $$
• Approximation $$C(r) = \sum_{i=1}^N T_i(1-\exp(-\rho_i\delta_i))c_i\qquad\text{and}\qquad T_i = \exp\bigg(-\sum_{j=1}^{i-1}\rho_i\delta_i\bigg)$$
• Positional encoding $$\gamma(p) = (\sin(2^0\pi p), \cos(2^0\pi p), \cdots, \sin(2^{L-1}\pi p), \cos(2^{L-1}\pi p))$$

This project was funded by DST-NGP (erstwhile NRDMS) .