Integrating COVID-19 compartmental models

and DL models

jabir and nelson

October 2021

The Idea

Its is well known that the prediction accuracy of neural networks is higher than

that of traditional prediction methods. This is primarily related to the neural

network’s features. Neural networks are good at capturing the properties of

complicated systems with high non-linearity that are difficult to represent using

a precise mathematical model, and they are also very adaptable. In-fact COVID-

19 dynamics within populations is a complex system with random mutation of

the virus and due to the complexity of social mobility. LSTM layer is a type of

Recurrent Neural Network (RNN) that utilizes learning from concurrent data.

Initially, we had this exciting idea of forecasting COVID-19 trends by pre-

dicting parameters of deterministic compartment based model for COVID-19

in each time step from trends in previous time steps using some deep learning

models. And then we the solve the compartmental model ODE’s to predict the

trends in the particular time step, and so on with the succeeding time steps.

But unfortunately, from a recent google search, we found that, people had al-

ready thought of it, and they had already done fantastic works based on this

idea, especially using LSTM, as in [1, 4]. And they have got very good results.

Therefore, we will try to give a short combined review of [1, 2, 3, 4] in this

report and propose to use the idea in our project.

Compartmental modeling for infectious dis-

eases

Regardless of the nature of transmissibility of human infectious diseases, the

individual life-course of infection can be conveniently represented by a sequence

of transitions between a few epidemiological classes, or compartments, triggered

by specific processes and parameters. For new pathogens, such as a pandemic

flu virus, all individuals are initially susceptible to the infection (class S), which

they acquire at a rate λ entering the exposed class (E), a latency or incubation

phase where individuals are infected, i.e. the virus is replicating in their body,

but not yet infective, which they become at some rate α. Individuals belonging

to the infective class (I) will usually recover, at a rate γ , acquiring immunity

and entering the removed class (R). Such modelling can be illustrated as shown

in Fig. 1

birth

λ(t)

birth

λ(t)

birth

λ(t)

Figure 1: The compartmental representation SEIRS, SIRS and SIS models for

some important classes of infections of individual course. The circles are identi-

fied epidemiological classes and arrows are marked as the process of class change,

entry and exit due to demographics.

Based on this illustration of the individual course, we can model the spread of

an infectious disease by describing the dynamics of infections at the population

level, by assigning a dynamic variable to each compartment denoting the number

(or the proportion) of individuals in that class at each instant of time. So, lets

denote the total population size and N, and X (S = X /N), H (E = H /N),

Y (I = Y /N), Z (R = Z /N) as the numbers (proportions) of individuals who

respectively occupy the various classes at time t, with N = X + H + Y + Z ,

and S + E + I + R = 1.

The population as a whole can be related to concept of homogeneous (or ran-

dom) mixing, which in this context, refers to an infection spreading by direct

person-to-person contacts in a closed homogenous social medium, the popula-

tion, whose agents have an approximately identical social activity. So, if C is

the number of contacts made by a susceptible individual per unit time, then

the probability that the contact made is with an infected individual is obviously

I = Y/N. And if β_I is the probability that the disease will be transmitted to

the susceptible individual from the infected individual, then the rate λ at which

individuals leave from the suceptible class S in Fig.

1 can be written as λ =

β_ICI. Setting β = β_IC, λ = βI.

Now, assuming that a population N has an unique and globally stable equilib-

rium N_e such that birth rate b(N_e) and mortality m(N_e) rate of the population

are the same, i.e., b(N_e) = m(N_e) = α, and that the population is at this steady

state, then we can translate the SEIRS diagram in Fig.

1 into the following

mean-field system of ODEs,

S^′ = µ(1 − S) + δR − βSI

(1)

E^′ = βSI − (α + µ)E

(2)

I^′ = αE − (γ + µ)I

(3)

complemented by R = 1 - S - E - I. Thus, the Model of Eqs. 1-3 is the so-called

deterministic SEIRS model.

2.1

SEIR modifications for COVID1-19

People had considered different modifications of SEIR model, such as adding

extra compartments as done in [4], or combining multiple SEIR models with

different parameters in-order to model spread between networks (eg. cites, house

holds, workplaces etc) as used in [1], specifically for modeling COVID-19 spread

with better accuracy.

Methodologies of incorporating DL models to

compartmental models

Ref.[3] where the first to propose a deep learning based solution for Covid-

19 spread prediction solely based on the known reported cases of Covid-19.

They designed a deep neural network, which consist of LSTM (Long Short

Term Memory) layer, dropout layer, and fully connected layers, to analyze the

reported Covid-19 cases and predict the possible future scenarios for the spread

in China, Europe, Middle East and worldwide. Their approach predicts the

cumulative number of cases, cumulative number of deaths and daily new cases

worldwide. All their predictions are done for the next 10 days given the actual

time series data of Covid-19. They evaluate their approach on the last 3 days

of actual data using Root Mean Square Error (RMSE) metric. They present

results from the networks that give the minimum RMSE values. Thus, the

network with minimum RMSE is used to predict the future scenarios. As new

data arise daily, the network can be re-train in order to adjust the real-time

predictions. Further, they present the deep neural network used for forecasting

and evaluate their approach with RMSE, and finally illustrate and discuss the

possible scenarios for Covid-19 spread regionally and worldwide.

[2] also uses

the similar and improved approach.

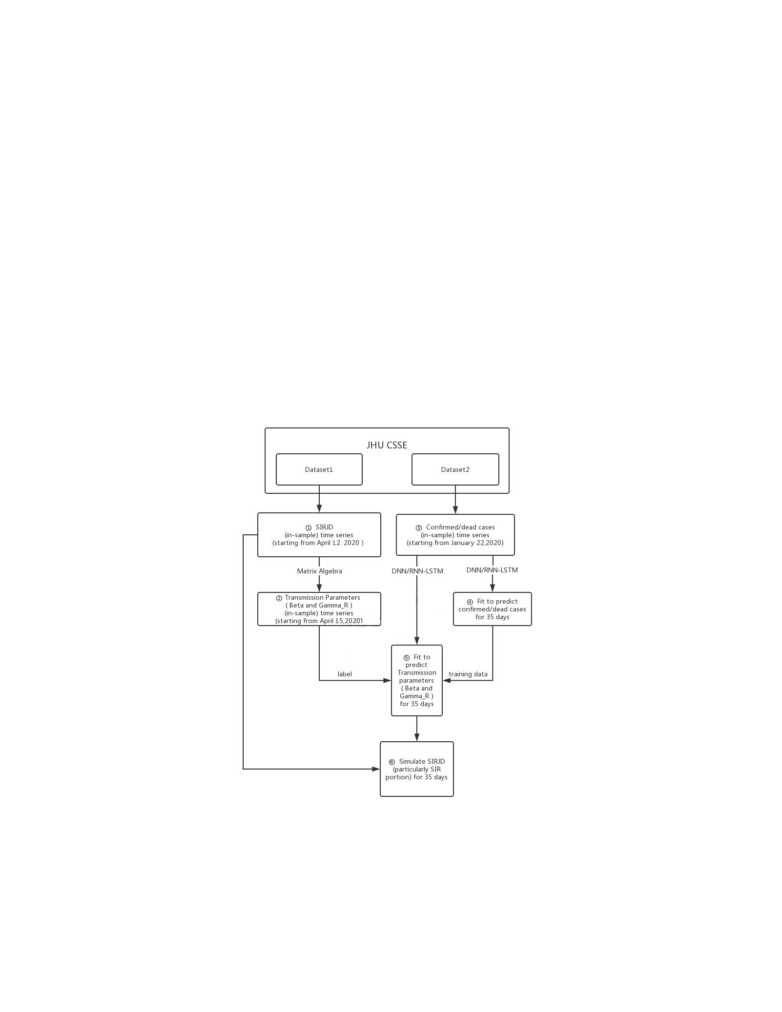
Now coming to the idea we propose, [4] considers SIRJD model for COVID-

(a modified version of SIR model). They construct the in-sample SIRJD time

series to come up with an in-sample time series for β and γ (the most critical

daily transmission parameters). Further they constructed a confirmed/dead-

case time series from the starting date of their data set. Then they apply two

deep learning algorithms; the standard deep neural networks (DNN) and the

LSTM to fit the confirmed/dead in-sample time series and predict the out-of-

sample time series, that is further development of confirmed/dead cases for 35

and 42 days in their work. This confirmed/dead in-sample time series is then

used as training data and the in-sample β and γ time series from Step 2 as

training label. And then DNN and LSTM is applied again to predict β and γ

for 35 and 42 days (out-of-sample time series). And finally, the predicted (out-

of-sample) transmission parameters (β and γ) from the starting date is used to

simulate 35- and 42-day progressions (out-of-sample time series) of the SIRJD

model (particularly the SIR portion) in a recursive manner, starting with the

data point of the last time step from the in-sample SIRJD time series.

Fig.(2) shows the flow chart that [4] used to demonstrate their methodology.

Figure 2: Flow chart from [4]

Ref.[1] is also has the same approach as [4]. But they use a better epi-

demiological model (SEIR) for heterogeneous population, which is called the

meta-population model and they incorporate it with DNN and LSTM. The

framework of methodology in [1] is illustrated in Fig.(3)

Figure 3: Framework from [1]

The scope of the idea to our project

We had tried many regression based model, but we failed to get more consis-

tent and more realistic result. We are excited to explore more on this idea to

incorporate and test it in our project. But its quite challenging. Interestingly,

the meta-population model incorporated with DNN and LSTM in [1] seems to

be a very consistent approach with the objective of our project for state wise

prediction.

References

[1] Hybrid Deep Learning-Based Epidemic Prediction Framework of COVID-19:

South Korea Case, Firda Rahmadani and Hyunsoo Lee.

[2] Peipei Wang, Xinqi Zheng, Gang Ai, Dongya Liu, Bangren Zhu. Time se-

ries prediction for the epidemic trends of COVID-19 using the improved

LSTM deep learning method: Case studies in Russia, Peru and Iran,

Chaos, Solitons & Fractals, Volume 140, 2020, 110214, ISSN 0960-0779,

https://doi.org/10.1016/j.chaos.2020.110214.

[3] Worldwide and Regional Forecasting of Coronavirus (Covid-19) Spread using

a Deep Learning Model. Cem Direkoglu and Melike Sah.